La base sur les arbres
Nous allons ici voir la structure des arbres et des forêts, qui est fondamentale en informatique. On va ici voir les définitions de base sur les arbres et le code de Prüfer.
Un arbre est tout graphe connexe sans cycle.
Et un graphe sans cycle mais non connexe est appellé une forêt (car ca fait plusieurs graphes connexe sans cycle, donc plusieurs arbres).

Une feuille ou sommet pendant est un sommet de degré 1 (qui se trouve donc au bout d'un arbre).
Un arbre est une structure fondamentale en informatique par ce qu'elle est utilisée pour répertorier les fichiers, créer de stables de matières, des sortes de tri (heapsort), des expressions algébriques, des frameworks, etc.
Un arbre peut être compris comme un graphe hierarchique qui possède une racine duquel tous les autres sommets partent.
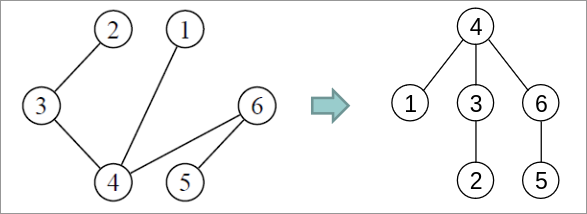
Par exemple dans l'image ci-dessus le sommet 4 au dessus de tous les autres peut être pris comme la racine, mais cela aurait très bien pu être le sommet 3 par exemple.
Pour représenter les liens entre les différents éléments on peut utiliser la terminologie généalogique tel que "père", "fils", "ancêtre", etc.
On peut également partitioner l'ensemble des sommets en rangs. Les rangs est la profondeur d'un élément par rapport à la racine. Par exemple la racine a un rang de 0, un enfant de la racine a un rang de 1, le petit enfant un rang de 2, et ainsi de suite.
La hauteur d'un arbre est la valeur de son plus grand rang.
Propriétés d'un arbre
Un graphe est un arbre si il respecte l'une des conditions suivantes (chaque condition est équivalente aux autres) :
- Le graphe est sans cycle et connexe
- Le graphe est sans cycle et comporte n-1 arêtes (où n est le nombre de sommets)
- Le graphe est connexe et comporte n-1 arêtes (où n est le nombre de sommets)
- Pour chaque paire de sommet est reliée par une seule chaîne simple (le graphe est donc sans boucle)
Cela signifie que si un graphe connexe et qu'il a n-1 arêtes où n est le nombre de sommets, alors le graphe est un arbre.
Egalement tout arbre avec au moins deux sommets comporte au moins deux feuilles.
Arbres binaires
On parle de n-arbre pour définir des abres où chaque sommet a au plus n enfants.
Un arbre binaire est donc un 2-arbre, ce qui signifie que chaque sommet peut avoir au plus 2 enfants.
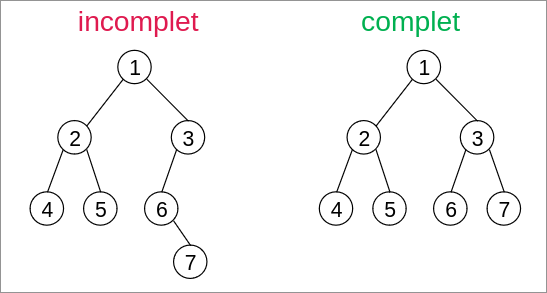
On dit qu'un arbre binaire est complet lorsque tous ses niveaux sont complètement remplis.
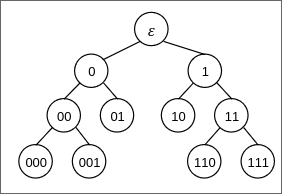
Les sommets d'un arbre binaire peuvent être appellé par des séquences binaires.
Un arbre binaire peut également être utilisé pour représenter des expressions algébriques, tel que celles-ci :
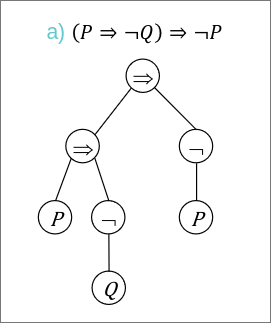
Dans ce type d'arbre les priorités d'opérations les plus élevées se trouveront en haut de l'arbre.
Parcours d'un arbre binaire
Il existe 3 types de manières de parcourir un arbre binaire.
- Le parcours préfixe qui consiste à visiter chaque sommet avant ses enfants. Donc on va visiter un sommet, puis visiter l'enfant de gauche de ce dernier, puis visiter l'enfant de droite de ce dernier.
- Le parcours postfixe qui consiste à visiter chaque sommet après ses enfants. Donc on va visiter l'enfant de gauche du sommet, puis visiter l'enfant de droite du sommet puis enfin visiter le sommet lui-même.
- Le parcours infixe qui sonsite à visiter chaque sommet entre ses enfants. Donc on va visiter l'enfant de gauche du sommet, puis on visite le sommet, puis on visite l'enfant de droite du sommet.
Arbres binaires de recherche (ABR)
Un arbre binaire de recherche est un arbre binaire où chaque enfant de gauche est plus petit (ou égal dépendant de l'ordre) que son parent, et chaque enfant de droite est plus grand que son parent (ou égal dépendant de l'ordre).
Cela peut notament être utile pour trier les éléments d'une suite. On met tous les éléments dans l'arbre, on peut alors ressortir une suite triée en faisant un parcours infixe sur l'arbre.