SnowCode

WIP : Cryptographie à clé secrète

Cette page de synthèse va parler de la cryptographie à clé secrète (cryptographie symmétrique)

Un cryptosystème symétrique est défini par une clé à garder secret qui sert à chiffrer et déchiffrer des messages grâce à une fonction de chiffrement et une fonction de déchiffrement.

La clé secrète est donc partagée uniquement de l'émetteur et du recepteur. Ce type de système est très ancien existe au moins depuis l'antiquité. Il est aussi améliorer par d'avantage de sécuirté grâce à la puissance de calcul des ordinateurs d'aujourd'hui.

Chiffre de César

Le chiffre de césar est simplement un décalage de lettre. La clé est donc simplement le décalage des lettres d'un certain nombre, à la base 3. Ainsi un A devient un C, un B devient un D, etc. Et une fois arrivé à Z, on recommence, donc un Z devient un B.

Cette méthode de chiffrement est très peu sûr mais est tout de même resté jusque dans les années 800.

Ce code peut être cassé très simplement par soit l'essai-erreur (il n'y a quand même que 26 clé possible), soit par l'analyse fréquentielle qui consiste à regarder quelles lettres apparaissent le plus souvent, et en déduire le décalage.

Par exemple, si on sait que le message chiffré est écrit en français et que la lettre la plus commune est le G, on peut en déduire que cette lettre doit en vérité être un E car c'est la lettre la plus commune en français.

On peut donc déduire que le décalage de E à G est 2, et décoder le message.

Chiffre de Vigenère

Le chiffre de Vigenère est une amélioration du code de César qui consiste à utiliser un ensemble de lettres comme clé.

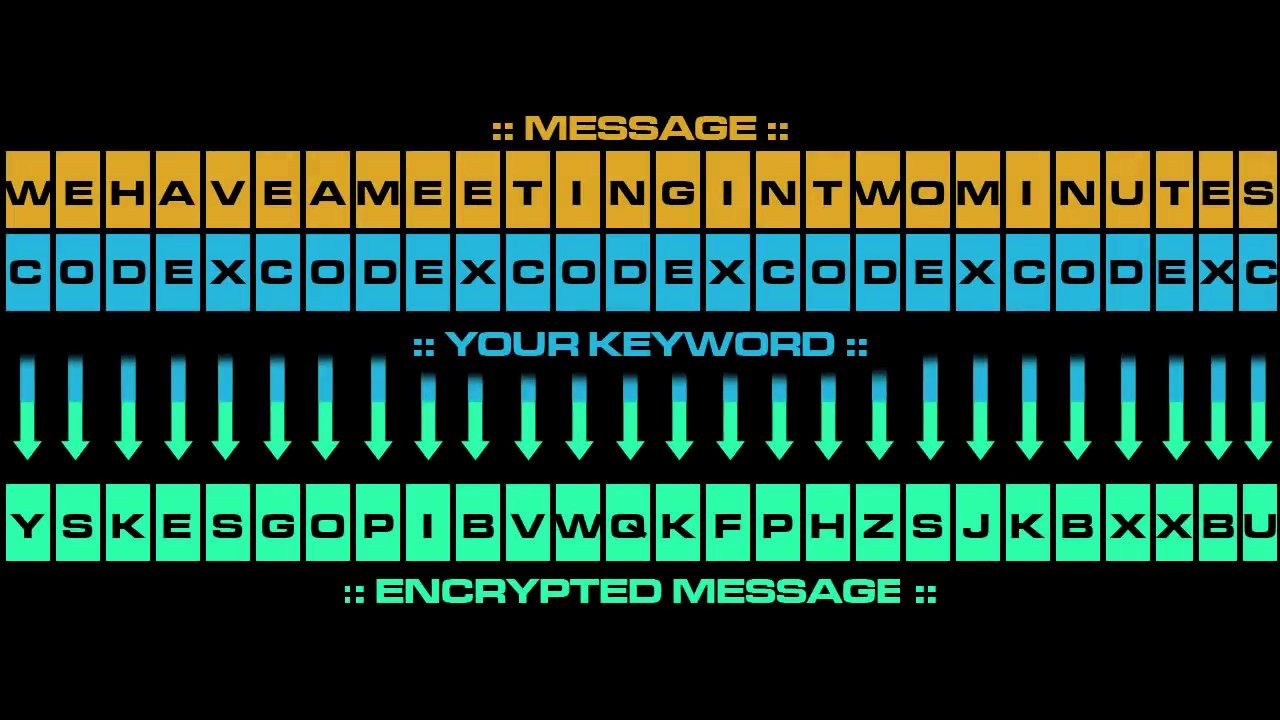
Exemplde de chiffre de vigenère

Cela consiste simplement à répeter la clé de façon à l'alonger à la taille du message, puis d'additioner les lettres. Ensuite on converi les lettres en chiffres de position dans l'alphabet (où A = 0 et Z = 25), puis on les additionne et on les retransforme en lettre. Par exemple : C + L = (3 + 11) % 26 = 13 % 26 = 13 = N, ou encore X + L = (23 + 11) % 26 = 34 % 26 = 8 = I

En répetant cette opération pour chaque lettre on obtient donc le cryptogramme, il suffit alors de faire l'opération inverse pour retrouver le message en clair. Par exemple I - L = (8 - 11) % 26 = -3 % 26 = 23 = X.

Il est possible de craquer le code de Vigenère en utilisant la méthode de Kasiski qui consiste à deviner la longueur de la clé en repérant des séquences de lettres répetées suseptible de correspondre à des mots courants. Ensuite on peut effectuer une analyse fréquentielle aux positions qui sont à un multiple de la longueur de la clé.

Substitutions homophonique

Un autre type de code est le code à substitution homophonique. Qui consiste à définir un code pour chaque lettre en fonction de sa fréquence dans la langue. Ainsi un E aura plus de code possibles associés.

Ensuite il suffit de remplacer chaque lettre par n'importe quel code de la liste pour la lettre. Ainsi cela rends impossible de faire une analyse fréquentielle sur le code.

PLAYFAIR

Playfair est un algorithme de chiffrement par substitution sur des digrammes. Voici en quoi il consiste :

Création de la matrice

  1. On prends une clé, exemple DANSEZ MAINTENANT JULES
  2. On supprime les doublons ainsi que la lettre J : DANSEZMITUL
  3. On complète avec le reste de l'alphabet (en évitant toujours les doublons et la lettre J) : DANSEZMITULBCFGHKOPQRVWXY
  4. On met cela dans une matrice carrée de 5 par 5
DANSE
ZMITU
LBCFG
HKOPQ
RVWXY

Chiffrement

  1. On trouve un message à chiffrer, par exemple DEMANDE RENFORTS IMMEDIATEMENT, on s'assure que le message n'a pas de lettre J
  2. On découpe le message par groupe de deux lettres DE MA ND ER EN FO RT SI MM ED IA TE ME NT
  3. Si un groupe a deux fois la même lettre, on interpose un X : DE MA ND ER EN FO RT SI MX ME DI AT EM EN T
  4. Si une lettre est seule, on ajoute un X : DE MA ND ER EN FO RT SI MX ME DI AT EM EN TX
  5. Ensuite pour chaque groupe de deux lettres, on regarde dans la matrice où elles sont.
    • Si les deux sont sur la même ligne, on prends la lettre immédiatement à droit de chaque lettre
    • Si les deux sont sur la même colonne, on prends la lettre immédiatement en dessous de chaque lettre
    • Sinon, on considère les deux commes les coins opposés d'un rectangle et on prends la lettre du coin opposé verticalement
  6. On obtient un certain résultat : AD BM SA YD DS PC ZX TN VT AU ZN MS UA DS FS

Déchiffrement

  1. Pour chaque élément du message à déchiffrer, on procède dans l'inverse du processus de chiffrement
    • Si les deux sont sur la même ligne, on prends la lettre immédiatement à gauche de chaque lettre
    • Si les deux sont sur la même colonne, on prends la lettre immédiatement en haut de chaque lettre
    • Sinon, on considère les deux commes les coins opposés d'un rectangle et on prends la lettre du coin opposé
  2. On supprime les éventueles X en trop dans le résultat du message et on ajoute les éventuels J manquant

ADFGVX

Matrice ADFGVX utilisée pour l'exemple

Chiffrement

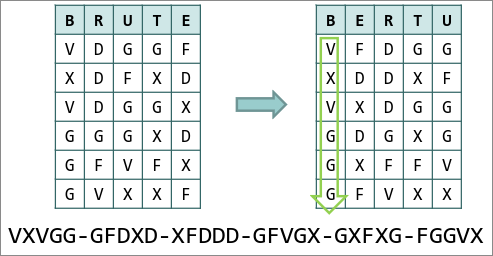
  1. On trouve un message à encoder, exemple DEMANDE RENFORTS
  2. Pour chaque lettre, on trouve quel est sa correspondance ligne-colonne dans la matrice. Par exemple ici : VD-GG-FX-DF-XD-VD-GG-XG-GG-XD-GF-VF-XG-VX-XF
  3. On écrit la clé dans une grille et on insère le résultat de l'étape précédente à l'intérieur
  4. On trie les colonnes par ordre alphabétique des lettres de a clé
  5. On concatène chaque colonne après éventuellement avoir ajouté un A de remplissage dans le tableau

Résultat transposition de adfgvx

Déchiffrement

  1. On divise le nombre de caractère du code par le nombre de caractère de la clé, ce qui arrondi à la hausse donne le nombre de ligne de la grille
  2. On écrit la clé avec ses lettres triée par ordre alphabétique
  3. On ajoute le message chiffré par colonne
  4. On trie les colonnes pour revenir à la clé de départ
  5. On cherche la correspondance de chaque couple dans la matrice pour revenir au message de départ