Arbres couvrants et coloration
Nous allons ici voir ce que sont les arbres couvrant, les arbres couvrant minimaux, et la coloration de graphe.
Un arbre couvrant (ou arbre maximal) est un graphe partiel qui est aussi un graphe.
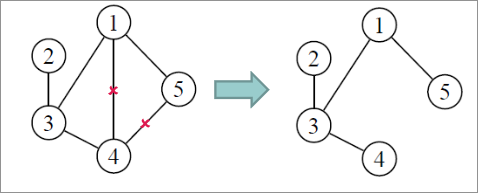
On peut également avoir un arbre couvrant de poids minimum lorsqu'un graphe est pondéré où le but est de trouver un arbre couvrant où la somme des pondérations est minimale.
Pour constuire un arbre couvrant de poids minimum, on peut utiliser l'aglgorithme de Kruskal.
Cet algorithme consiste simplement à trier les arêtes par leur poid, et les ajouter dans l'ordre dans que cela ne forme pas de boucle.
Coloration
La coloration des sommets d'un graphe consiste à colorier des sommets dans le nombre minimal de couleurs possible de sorte que deux sommets adjacents ne soient pas de la même couleur.
On appelle stable un ensemble de sommets qui ne sont pas adjacents.
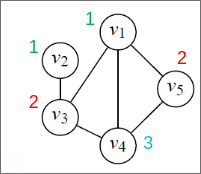
On parle de cardinal d'un stable pour décrire sa longueur. Et le stable le plus long d'un graphe (donc qui a le cardinal le plus élevé) est apellé le nombre de stabilité.
Donc pour faire la coloration d'un graphe il suffit donc de trouver un ensemble de stables (partition), qui reprends l'ensemble des sommets.
Pour faire la coloration minimale d'un graphe il faut donc avoir la partition complète la plus minimale possible (donc qui comprends tous les sommets mais qui contient le plus petit nombre de stables).
Le nombre chromatique d'un graphe représente le nombre de couleur minimale pour colorer les sommets du graphe. C'est donc le nombre de stable de la partition complète minimale de coloration.
Trouver le nombre chromatique par encadrement
Il est possible de trouver des indications sur le nombre approximatif de couleurs nécessaires pour colorer un graphe en estimant le nombre chromatique sur base de quelques règles.
Une première règle est que le nombre chromatique sera toujours plus petit ou égal au plus grand degré des sommets plus 1. Cette règle peut être représentée par la formule suivante où r représente le plus grand degré de sommet et \( \gamma(G) \) représente le nombre chromatique.
$$\gamma(G) \le r + 1$$
Cette règle peut être exemplifiée par un graphe complet de 5 sommets, où le degré le plus élevé est 4 (chaque sommet connait les 4 autres sommets du graphe). Et puis ce que chaque sommet est adjacent à chaque autre sommet le nombre chromatique doit être 5, soit le degré le plus élevé + 1.
Un autre type de majoration (estimation de la borne haute des possibilité du nombre chromatique) est d'utiliser le nombre de stabilité. Cette règle est représentée par la formule suivante où "n" représente le nombre de sommets.
$$\gamma(G) \le n + 1 - \alpha(G)$$
Cette règle peut être expliquée par le fait que le nombre de stabilité représente le plus grand stable, et que chaque sommet d'un stable peut être coloré d'une même couleur puis ce qu'ils ne sont pas adjacents. Par conséquent le nombre de couleurs totale sera forcément le nombre de sommets - le nombre de sommets coloré par le stable + la couleur du stable.
Enfin on peut encadrer un nombre chromatique par minoration. On peut le faire en le comparant à la taille de la plus grande clique (plus grand sous-graphe complet). Il suffit alors de connaître le nombre de sommets dans la plus grande clique du graphe et on sait que le nombre de couleurs (nombre chromatique) sera forcément plus élevé puis ce que dans un graphe complet il faut toujours autant de couleurs qu'il n'y a de sommets.
Cette règle peut être représentée par la formule suivante, où \( \omega(G) \) est l'ordre (nombre de sommets) de la plus grande clique (sous-graphe complet) :
$$\gamma(G) \ge \omega(G)$$
Attention Je trouve que le chapitre sur la coloration est assez complexe du coup je passe à autre chose pour le moment pour y revenir plus tard, il faut donc considérer que cette partie n'est pas complète. Elle devrait cependant être suiffisante pour faire les exercices de coloration disponible sur la plateforme.