SnowCode

Ceci est le début de la synthèse sur les graphes orientés.

En donnant un sens aux arêtes d'un graphe on obtient un digraphe, aussi appellé graphe orienté.

Cela signifie donc que les arêtes à la place d'être un ensemble non-ordonné de 2 sommet, est un ensemble ordonné de 2 sommets.

Il y a donc 3 types de degré pour un sommet dans un digraphe

• Le degré (( d^+ \) qui est le degré extérieur, soit le nombre d'arcs qui vont du sommet vers un autre
• Le degré (( d^- \) qui est le degré intérieur, soit le nombre d'arcs qui vont d'un autre sommet vers celui-ci.
• Le degré total (\( d \)) comme la somme des degrés extérieur et intérieur.

Pour décrire les voisins d'un sommet on parle de prédécesseurs (pour ceux où un arc part depuis eux vers le sommet courant) et de successeurs (pour ceux qui sont au bout d'un arc qui part depuis le sommet courant).

Tout comme pour les graphes non-orienté il existe des cycles et des chaines. Sauf que dans les graphes orientés un cycle est appellé un circuit et une chaîne est appellée un chemin car elle doit suivre une certaine direction indiquée par les arcs.

On parle de graphe acyclique lorsqu'un graphe ne contient aucun circuit.

Connectivité des graphes orientés

Commes les arêtes sont maintenant des arcs qui ont une direction, la connectivité des graphes devient un peu plus floue.

• Un graphe est dit fortement connexe si il est possible de tracer un chemin vers n'importe quel sommet
• Un graphe est dit faiblement connexe lorsqu'il est possible de tracer une chaine vers n'importe quel sommet (mais cette chaine n'est pas dirigée dans le bon sens)
• Un graphe est dit non connexe dans tous les autres cas

Orientation d'un graphe

Une orientation d'un graphe non-orienté est un graphe orienté obtenu en fixant un sens aux arêtes d'un graphe non-orienté.

Un graphe non-orienté est dit fortement orientable lorsqu'il est possible de trouver une orientation du graphe qui permette d'obtenir un digraphe fortement connexe.

Représentation de graphes orientés

Il est possible d'utiliser les même formes (matrices et listes) pour représenter des graphes fortement orientés.

La différence pour une matrice est que l'on ne va noter une intersection entre deux sommets si le sommet correspondant à l'indice de la ligne a un arc pointant vers le sommet correspondant à l'indice de la colonne.

Contrairement à un graphe orienté elle n'est donc pas symétrique. C'est-à-dire que que l'intersection de la ligne 3 avec la colonne 4 ne donnera pas la même chose que l'intersection de la ligne 4 et de la colonne 3.

Il en vas de même pour les listes d'adjacences où dans chaque liste on ne va noter que les sommets que l'on peut atteindre en suivant un arc depuis le sommet courant.

Digraphes sans circuits (acycliques)

Les digraphes sans circuits sont l'équivalent des arbres et des forêts dans les graphes non-dirigés.

On parle donc de rang pour chaque 'étage' du graphe en partant d'une racine donnée. Et puis ce que les liens entre les sommets (les arcs) sont dirigés, on sait que pour n'importe quelle arc, le rang du sommet qui est à sa source sera toujours inférieur à celui de sa destination.

On applle un arbre dirigé tout digraphe où il est possible de trouver un chemin depuis une racine donnée vers tous les autres sommets du graphe.

PERT

Si on part du tableau de tâche suivant :

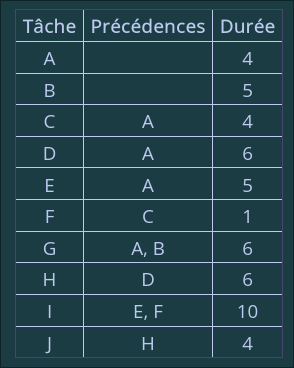
Création du graphe de départ

Tout d'abord on peut ouvrir GraphEditor, créer un nouveau graphe et choisir le type "PERT".

Ensuite on peut créer deux sommets, un premier qui correspondra au début du projet, et un deuxième qui correspond à la fin du projet.

Ensuite on peut ajouter un sommet qui correspondra à chaque précédence possible.

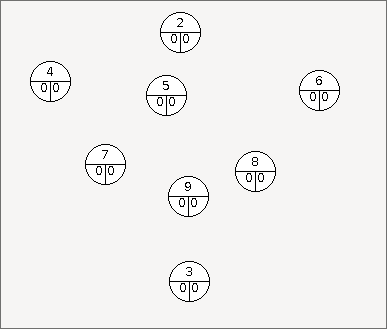
Dans cet exemple, 4 correspond à la précédence A, 5 à la précédence C, 6 à la précédence A+B, 7 à la précédence D, 8 à la précédence E+F et enfin 9 à la précédence H.

Ensuite on peut relier les arcs (les tâches) en précisant leur lettre + leur durée en les liant depuis leur précédence vers la précédence dont ils vont faire partie.

Les tâche sans successeurs seront liées à la fin de projet, et les tâches sans prédesseurs partiront du premier sommet.

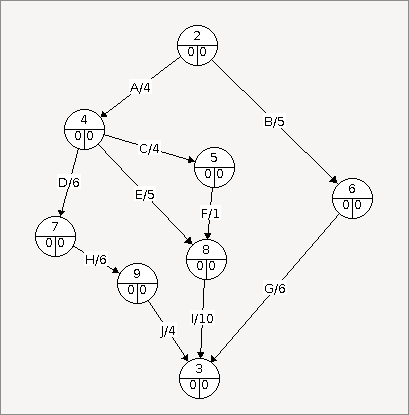
Dans le graphe précédent, il manque cependant quelque chose, on peut voir que le sommet 6, censé correspondre à A+B ne correspond qu'a B. Il faut donc pouvoir ajouter une dépendence depuis A à l'aide d'une tâche fictive.

Pour cela on va ajouter une tâche nommée "X" de durée 0 qui va du précédent A (sommet 4) au précédent A+B (sommet 6)

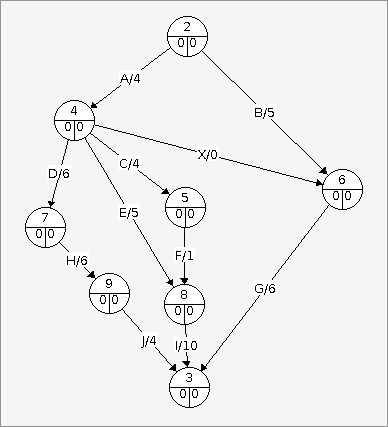
Pour finir la construction du graphe il faut encore s'assurer que toutes les directions vont vers le bas afin de pouvoir numéroter les sommets par étage.

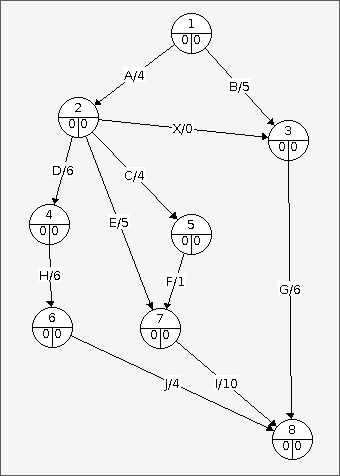
Assignation des valeurs de début

La valeur de début du premier sommet est 0.

Pour chaque sommet dans l'ordre des numéros, on va regarder chaque précédente du sommet et regarder lequel a la durée + début le plus élevé. Cette valeur deviendra alors la valeur de début du sommet.

Donc si un sommet a 2 précédents, la tâche B (durée = 5, début = 0) et la tache X (durée = 0, début = 4), alors la valeur de début sera 5 car 5+0 est plus grand que 4+0.

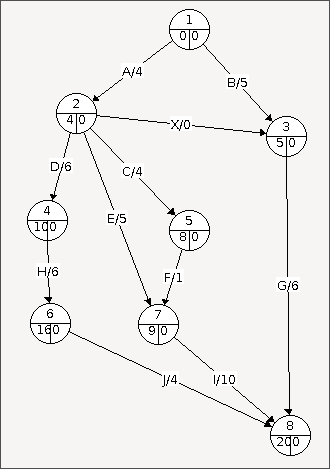
Assignation des valeurs de fin

La valeur de fin du dernier sommet sera la même que celle de début.

Ensuite, pour chaque sommet à partir de l'avant-dernier, pour chaque successeur du sommet, on regarde la date de fin du successeur - la durée. La valeur la plus minimale sera la date de fin du sommet actuel.

Donc si on a un sommet qui a 4 successeurs : la tâche X (durée = 0, fin = 14), la tâche C (durée = 4, fin = 9), la tâhce E (durée = 5, fin = 10) et la tâche D (durée = 6, fin = 10). On aura une date de fin de 4, car 10-6 est la différence la plus petite comparée à 10-5, 9-4 ou 14-0.

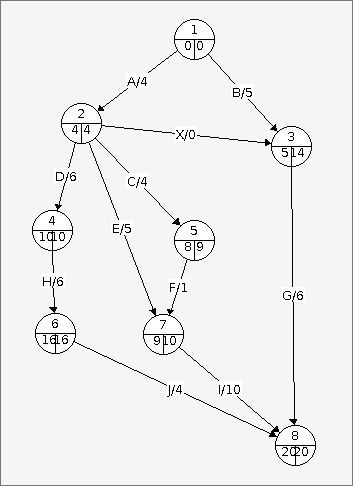
Trouver le chemin critique

Le chemin critique est le chemin qui contient toutes les tâches les plus critiques pour le projet. Donc toutes les tâches qui, si elles prennent du retard, entraine un retard sur l'ensemble du projet.

Les tâches/arc critiques sont celles qui connecte les sommets ayant la même date de début et de fin.

Ces arcs ont également comme propriété que leur durée est égale à la différence de date de début entre les deux sommets qu'elle connectent.

Dans GraphEditor, on peut alors mettre une épaisseur de 2 à tous les arcs/tâches qui font partie du chemin critique.

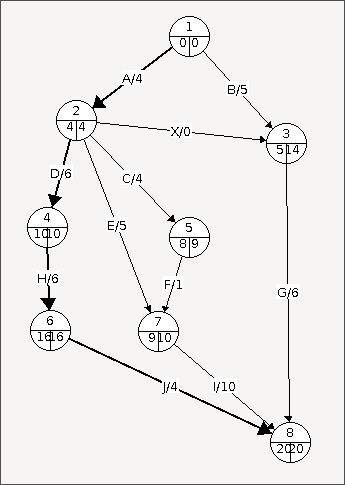
Et voilà, le graphe PERT est à présent tracé. On peut donc dire que les tâches critiques sont A, D, H et J.