SnowCode

Nous allons ici voir ce que sont les graphes partiels, les sous-graphes, les degrés, les chaines, les cycles, les graphes eulériens, les graphes hamiltoniens, les couplages et les graphes planaires.

Graphes partiels et sous-graphes

Un graphe est un graphe partiel d'un autre graphe lorsqu'il correspond à l'autre graphe mais avec des arêtes en moins (en d'autres termes, il a les même sommets, juste moins d'arêtes).

Un sous-graphe en revanche est une partie de graphe. Il s'agit donc d'enlever des sommets ainsi que toutes les arêtes incidentes (qui sont liées) à ces sommets.

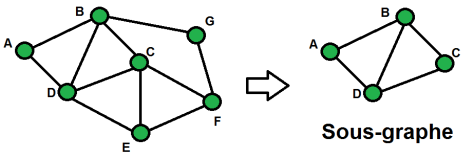
Un sous-graphe partiel désigne un graphe partiel d'un sous graphe (soit une partie d'un graphe plus grand, mais avec moins d'arêtes).

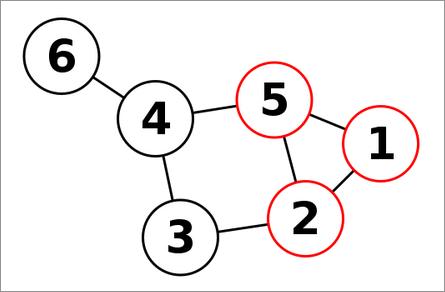
Une clique désigne un sous-graphe complet d'un graphe plus grand. Par exemple dans le graphe ci-dessous le sous graphe composés des sommets 5, 1 et 2 est une clique car ils sont tous liés entre eux directement.

Degré de sommets et de graphes

Le degré d'un sommet correspond au nombres d'arêtes qui lui sont incidente (qui le relie). Dans un graphe simple, le degré d'un sommet est donc simplement le nombre de voisins de ce sommet.

Si un sommet est relié à lui même, l'arête qui est liée à lui-même sera considéré comme 2.

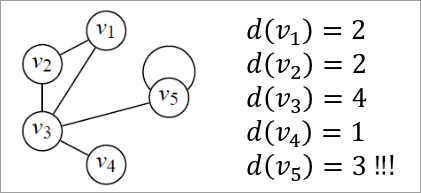
Il est possible de tirer certaines conclusions sur base des arêtes et des degrés. On sait par exemple que la somme des degrés des sommets d'un graphe correspond à deux fois le nombre d'arête car chaque arête contribue pour 2 sommets (donc 2 degrés).

Egalement un graphe simple aura toujours un nombre pair de sommets de degré impair.

Le degré d'un graphe est le degré maximum de tous ses sommets. Donc si le plus haut degré de sommet d'un graphe est 4, le degré du graphe sera 4.

On parlera de k-régulier où k est le degré, pour définir un graphe où tous les sommets ont le même degré.

Pour donner un exemple concret de ce principe, les degrés peuvent nous aider à résoudre cette situation :

Est-il possible de relier 15 ordinateurs de sorte que chaque appareil soit relié avec exactement trois autres ?

La situation peut être représenté par un graphe simple où chaque sommet est un ordinateur et chaque connexion est une arête.

Si chaque sommets est relié à 3 autres, alors chaque sommet aura un degré de 3, ce qui est impossible au vu du théorème vu plus tot qui dit que Un graphe simple aura toujours un nombre pair de degré impair. Ici il y a un nombre impair (15) de sommets qui ont un degré impair (3).

Chaînes et cycles

Une chaîne dans un graphe est une suite de sommets encadré par des arrêtes. Par exemple 1 - 2 - 3 - 4 (où les nombres sont des sommets, et les tirets sont des arêtes).

La longueur de la chaine correspond au nombre d'arrête. Pour l'exemple donné plus tot, la longueur de la chaine est donc 3.

La distance entre deux sommets, correspond à la longueur de la plus petite chaîne permettant de les relier.

Le diamètre d'un graphe correspond à la plus longue distance entre deux sommets du graphe.

Une chaîne est dite élémentaire si chaque sommet y apparait au plus une fois, en d'autres termes, si on ne passe jamais 2 fois par le même sommet.

Une chaine est dite simple si chaque arète apparaît au plus une fois (on ne passe pas 2 fois par la même arête).

Une chaîne où les sommets de départ et de fin est appellée une chaîne fermée. Et une chaîne fermée simple (où on ne passe qu'une seule fois sur chaque arrête) est appellée un cycle.

Cette définiton de cycle permet égalmeent de définir les graphes biparti. Un graphe biparti peut être défini comme un graphe qui ne contient aucun cycle de longueur impaire.

Graphes, chaine et cycles eulériens

Un cycle eulérien est un cycle passant une seule fois par chacune des arêtes du graphe.

Un graphe eulérien est un graphe possédant un cycle eulérien.

Une chaine eulérienne est une chaîne passant une seule fois par chacunes des arêtes du graphe.

Un graphe semi-eulérien est un graphe ne possédant que des chaînes eulériennes.

Il est possible de savoir si un graphe est eulérien ou semi-eulérien très facilement :

• Si le graphe est connexe et possède exactement deux sommets de degré impair, alors il est semi-eulérien
• Si le graphe est connexe et possède uniquement des sommets de degré pair, alors il est eulérien

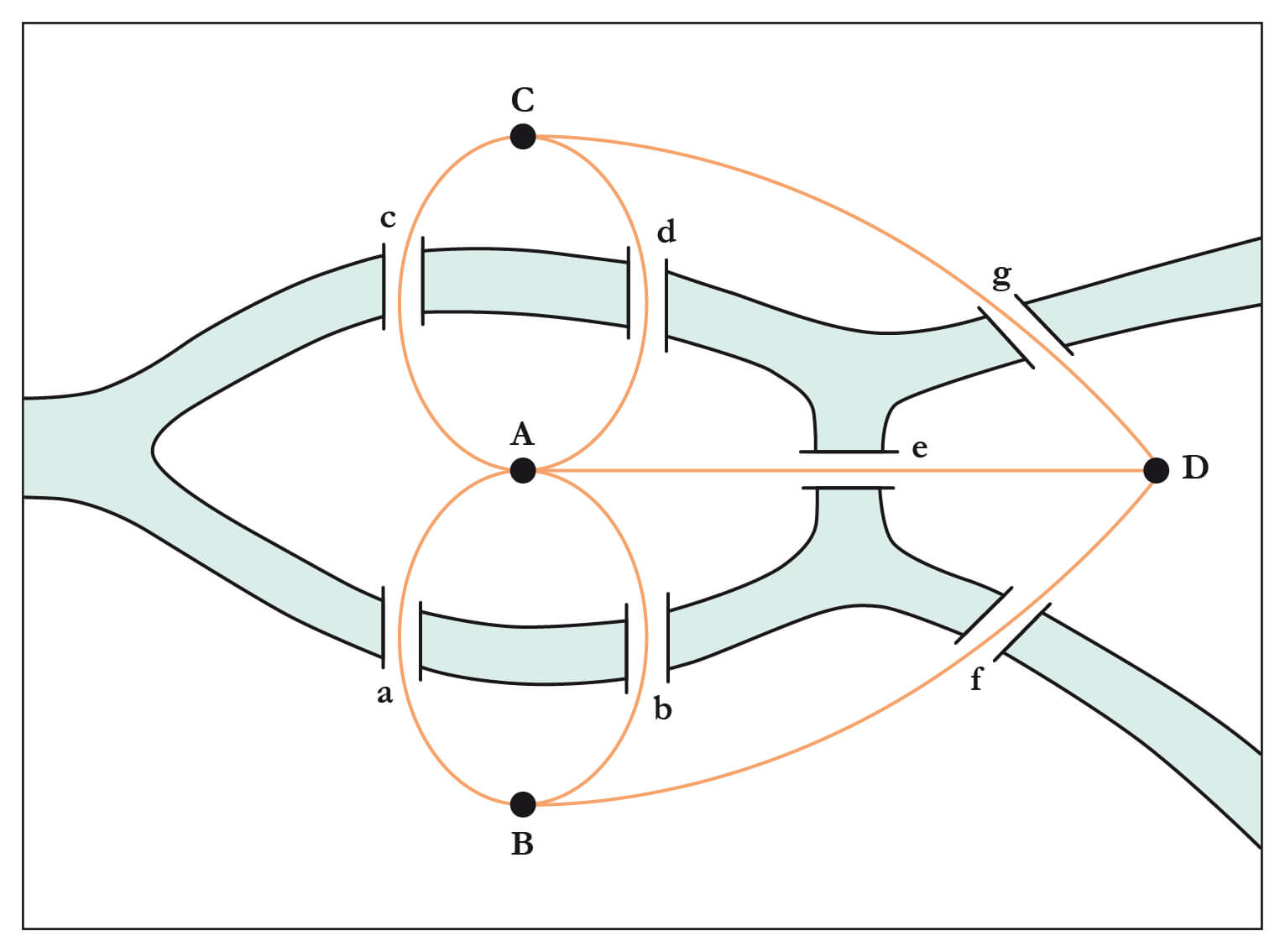
Grâce à ces informations il est donc possible d'expliquer pourquoi le problème des 7 ponts de Königsberg (représenté ci-dessus) n'a pas de solution.

Le problème est de trouver un chemin qui permet de retourner à son point de départ en passant par chaque pont de la ville.

On peut voir que toutes les îles ont un nombre impair de ponts (C en as 3, D en as 3, B en as 3 et A en as 5), il ne rempli donc ni la condition pour être semi-eulérien, ni la condition pour être eulérien.

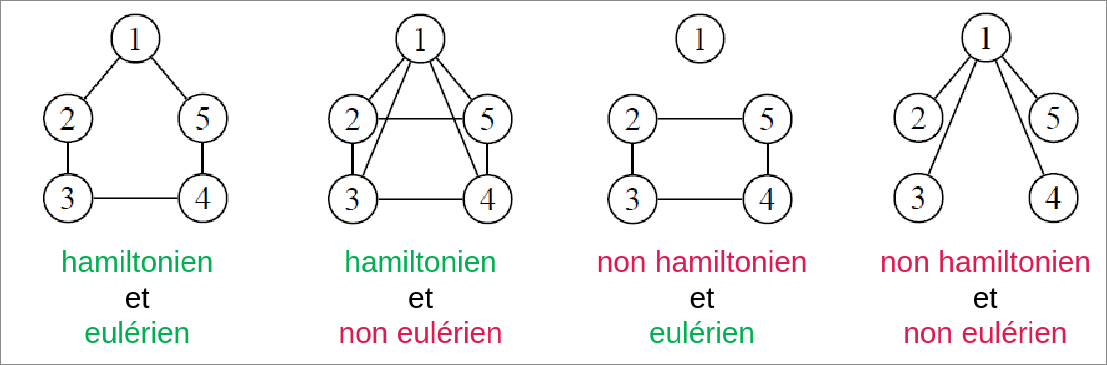
Graphes, chaine et cycles hamiltoniens

Un cycle hamiltonien est un cycle passant une seule fois par chacun des sommets du graphe.

Un graphe hamiltonien est un graphe qui possède un cycle hamiltonien.

Une chaîne hamiltonienne est une chaîne passant une seule fois par chacun des sommets du graphe.

Un graphe semi-hamiltonien est un graphe ne possédant que des chaînes hamiltoniennes.

Si le graphe possède un sommet de degré 1, alors le graphe ne peut pas être hamiltonien. Si le graphe possède un sommet de degré 2, alors les deux arrêtes incidentes à ce sommet doivent faire partie du cycle. Tous les graphes complets sont hamiltoniens.

Il n'existe pas de caractérisation simple des graphes semi-hamiltoniens.

Couplage

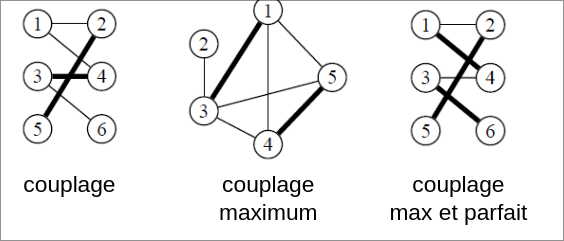
Un couplage de graphe est un sous-graphe (partie du graphe) partiel (auquel il manque des arêtes) 1-régulier (chaque sommet à un seul voisin) de celui-ci.

En somme un couplage est constitué de 2 sommets et un ou plusieurs arêtes entre les deux. Il doit être impossible de lier des couplages entre eux, donc chaque sommet peut faire partie de maximum un seul couplage.

Un sommet faisant partie d'un couplage est dit saturé (et dans le cas contraire, il est dit insaturé).

Un couplage maximum contient le plus grand nombre possible d'arrête.

Un couplage parfait est un couplage où chaque sommet du graphe est saturé.

Une chaîne alternée est une chaîne élémentaire (où on ne passe qu'une seule fois par chaque sommet) qui alterne à chaque fois entre une arrête dans un couplage, et une arrête hors du couplage.

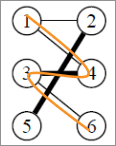
Une chaîne augmentante est une chaîne alternée qui relie deux sommets insaturés. C'est notament l'exemple du cas au dessus car on relie le sommet 1 et 6 qui sont tous les deux insaturés.

Par définition un couplage est maximum (tous les sommets sont saturés) uniquement si il n'y a pas de chaine augmentante relative au couplage (pas de sommets insaturés).

Graphes planaires

Comme dit plus tot un graphe est dit planaire si il est possible de le dessiner dans un plan en 2D de sorte que ses arêtes ne se croisent pas (à savoir que les arêtes ne sont pas forcément droites).

Une carte ou un graphe planaire topologique est une représentation graphique qui satisfait cette condition.

Une carte divise le plan en plusieurs régions, par exemple les lettres représentes les différentes régions dans la carte ci-dessous :

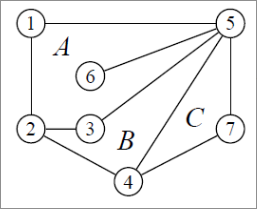
Le degré d'une région (noté d(r)) est la longueur de chaîne fermée minimum passant par tous les sommets qui délimitent la région.

Par exemple dans la carte vue plus tot, la région A a un degré de 6 car la longueur de la chaine 1 - 5 - 6 - 5 - 3 - 2 - 1 est 6.

La sommes des degrés des régions d'une carte connexe (carte d'un graphe connexe) correspond à deux fois le nombre d'arêtes du graphe.

Il existe égalmenet une relation (relation d'Euler) entre le nombre de sommets (S), le nombre d'arêtes (A) et le nombre de régions (R). Cette relation est S - A + R = 2.

Par exemple dans le même exemple vu plus tot, il y a 7 sommets, 9 arêtes et 4 régions, soit 7 - 9 + 4 = 2.

Un graphe est non planaire si il contient un sous-graphe homéomorphe (?) au graphe biparti K3,3 ou au graphe complet K5.

Grâce à cela il est donc possible de savoir si un graphe est planaire ou non.

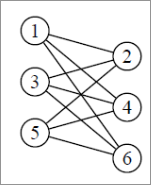
Par exemple si on veut prouver que le graphe ci-dessus n'est pas planaire :

Le graphe a 6 sommets et 9 arrêtes, selon la relation d'Euler, on peut donc en déduire qu'il doit y avoir 5 régions.

On peut aussi savoir que le degré total de toutes les régions correspond à 2 fois le nombre d'arrêtes. Donc dans ce cas, 18.

Ensuite on peut essayer de trouver la longueur de chaine fermée minimum du graphe (par exemple 1-2-3-4-1) qui est donc d'une longueur de 4. Sauf que si on suppose que toutes les régions font cette longueur minimale, alors la somme ferrait 5 (le nombre de régions) fois 4 (la longueur minimale), ce qui donnerait 20 et pas 18 comme ça devrait l'être normalement.