SnowCode

Nous allons ici voir différnetes manières de représenter un graphe de manière non-graphiques. Il existe notament de moyens pour s'entrainer sur ceux ci sur la page de cours.

Matrice d'adjacence

Il est possible de représenter un graphe simple par une matrice d'ajacence où chaque ligne et chaque colonne représente un sommet.

Dans un graphe simple (non pondéré), si il existe un lien entre deux sommets, on va trouver le croisement des deux et y indiquer un 1, sinon on indique 0.

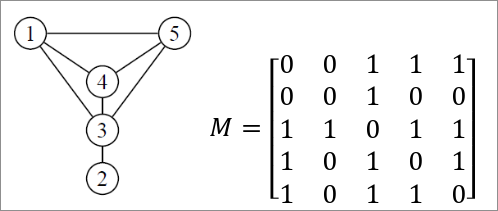
La diagonale a toujours des zéros à moins qu'il existe une boucle d'un sommet vers lui-même.

Les matrices d'ajacence ont l'avantage de permettre de savoir très simplement si une adjacence existe entre deux sommets. Il suffit de voir leur croisement dans la matrice.

Les matrices d'ajacence ont cependant le désavantage de nécessiter plus de stockage puis ce qu'il faut également stocker les adjacences qui n'existe pas (avec un 0). Le stockage nécessaire est donc S^2 (si il y a 5 sommets, il faudra 25 unités de stockage).

Liste d'adjacence

Il est aussi possible de représenter un graphe simple en donnant la liste des sommets qui lui sont adjacent.

Ces listes sont généralement ordonnée du sommet avec le nombre le plus petit, au sommet avec le nombre le plus grand.

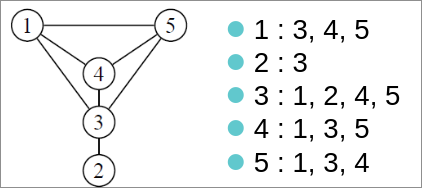
Les listes d'adjacence ont l'avantage d'être plus compacte que les matrices d'ajacence car elles ne stoquent que les adjacences qui existe réellement.

Elles ont cependant le désavantage d'être beaucoup moins efficace à chercher des adjacence entre deux points car il faut itérer toute la liste d'un sommmet (si un sommet a beaucoup d'adjacence, cela peut donc prendre beaucoup de temps).