Introduction sur la théorie des graphes
Première partie du cours sur la théorie des graphes, où on va voir les premières notions de graphes.
Premières définitions sur les graphes
Un graphe fini est défini comme un ensemble de sommets (vertices) et un ensemble d'arêtes (edges).
Chaque arête est définie comme une paire non ordonnée de sommets. Les sommets dans une arête sont appelé des extrémités.
Si deux sommets sont reliés par une arête on dit qu'ils sont adjacents et ont dit que l'arête est incidente.
Le nombre de sommets définit l'ordre du graphe. Ainsi un graphe de 3 sommets, sera ainsi définit comme un graphe d'ordre 3.
Représentations graphiques d'un graphe
Si on souhaite définir un graphe sans qu'aucune de ses arêtes ne se croise, on dit que le graphe est planaire.
Il est important de savoir qu'un graphe est un concept théorique, il y a donc une infinité de représentations graphiques possibles pour un même graphe.
Voici par exemple un même graphe avec deux représentations. Le fait que dans la deuxième représentation, aucune arête ne se touche indique que le graphe est planaire.
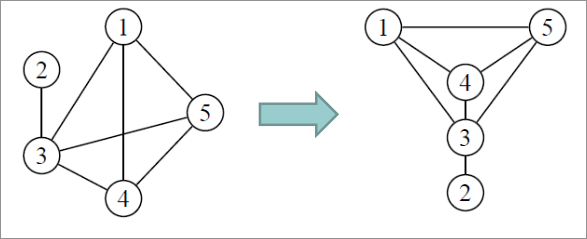
Types de graphes
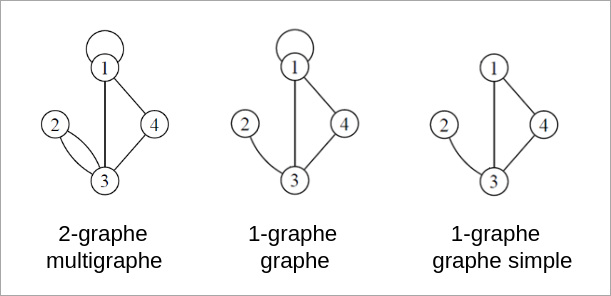
Un graphe simple est un graphe où maximum une arête relie deux sommets et où il n'y a pas de boucles sur un sommet.
A l'inverse il y a le multigraphe qui est un graphe où il peut y avoir plusieurs arêtes entre deux même sommets et où une arête peut relier un sommet à lui-même.
Pour les graphes il existe la notation p-graphe où p représente le nombre d'arête maximum entre deux sommets. Par exemple si il y a au plus deux arêtes entre deux sommets, on dira que c'est un 2-graphe.
Le plus souvent on étudira des 1-graphe.
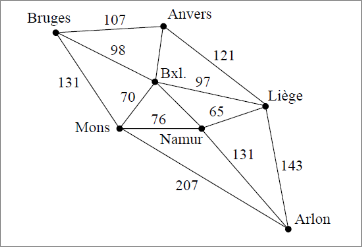
Un graphe est pondéré si des valeurs sont associées aux arêtes. La valeur associée à une arête est appellée le poids de l'arête.
Connectivités des graphes
Un graphe est dit connexe lorsqu'il est possible de trouver un chemin pour relier n'importe quel sommet à n'importe quel autre sommet. En d'autres termes cela signifie que tous les sommets sont connectés d'une manirèe ou d'une autre.
A l'inverse un graphe non connexe peut être décomposé en composantes connexes.
Une arête est appellée un pont si sa suppression augmente le nombre de composantes connexes du graphe.
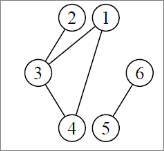
Le graphe ci-dessus est un graphe non-connexe car il est impossible de relier 6 à 1 par exemple car 5 et 6 forme un groupe à part du graphe.
Si sur le graphe ci-dessus, on supprime l'arête reliant 2 et 3, 2 se retrouve déconnecté du reste, par conséquent le nombre de composantes connexes augmente. Il en va de même pour l'arête 5 à 6. Ces deux arêtes sont donc des ponts dans le graphe.
Graphes complets et biparti
Un graphe est dit complet si chaque sommet du graphe est relié directement à tous les autres sommets.
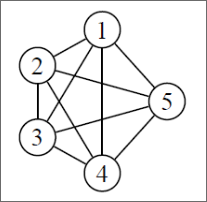
Un graphe complet est souvent représenté avec la notation K ainsi un graphe complet K5 signifie qu'il s'agit d'un graphe complet à 5 sommets.
Un graphe est dit biparti si ses sommets peuvent être divisés en deux ensembles de sorte que les sommets d'un ensemble n'ont d'arrête que vers des sommets de l'autre ensemble.
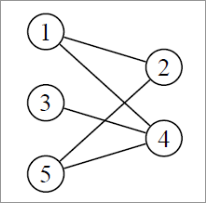
Le graphe ci-dessus est biparti car les sommets 1, 3 et 5 ne sont pas reliés entre eux mais mais on des liens vers des sommets de l'ensemble 2 et 4. Il en va de même pour 2 et 4 qui sont liés aux sommets de l'ensemble 2,3,5 mais pas entre eux.
Enfin il existe les graphes biparti complèts lorsque chaque sommet de chaque ensemble est connecté à tous les sommets de l'autre ensemble.